Lernregel
4.1 Lernalgorithmus
Die Backpropagation-Lernregel ist die mit Abstand
am häufigsten verwendete Lernregel. Daher ist es ratsam,
sich näher mit ihr zu befassen. Dazu hier eine kurze
Übersicht über die wesentlichen Schritte des Lernens,
die nachfolgend genauer erläutert werden.
- Initialisierung
- Feed-Forward
- Fehlerberechnung
- Fehler-Backpropagation
4.2 Initialisierung
Zu Beginn muß dafür Sorge getragen werden, dass die Gewichte
und Schwellwerte des Netzes unterschiedliche Werte erhalten.
Wenn die Neuronen einer Schicht die gleichen Parameter besäßen,
würde das dazu führen, dass sich die gesamte Schicht wie ein
einziges Neuron verhält. Die Lösbarkeit einer Aufgabe ist abhängig
von der Anzahl der Neuronen. Wenn sich eine ganze Schicht verhält
wie ein einziges Neuron, so kann man davon ausgehen, dass man
keine praktikable Lösung findet.
4.3 Feed-Forward
Die Abbildung 2.5 zeigt ein sehr stark vereinfachtes Netz.
Man kann erkennen, dass am Eingang ein n-dimensonaler x-Vektor
anliegt. Jedes x-Element des x-Vektors steht einem Neuron gegenüber.
Diese Neuronen bilden die erste Schicht. Die erste Schicht wird
Eingabeschicht genannt. Die nachfolgende Schicht besteht aus
q Neuronen. Da man nicht direkt auf sie zugreifen kann, wird diese
Schicht auch verborgene Schicht genannt. Die Ergebnisse aller Neuronen
der Eingabeschicht werden an jedes einzelne Neuron der verborgenen
Schicht weiter gegeben. Die Neuronen der verborgenen Schicht geben
ihrerseits ihre Ergebnisse an jedes einzelne Neuron der Ausgabeschicht
weiter. Die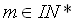 Ausgabeneuronen liefern den m-dimensonalen Ausgabevektor
Ausgabeneuronen liefern den m-dimensonalen Ausgabevektor
des Netzes. Der bis jetzt beschriebene Vorgang ist bekannt unter
dem Namen Feed-Forward. Feed-Forward beschreibt die Berechnung,
die das Netz von vorne bis nach hinten durchläuft. Dabei fällt auf,
dass innerhalb einer Schicht die Neuronen prinzipiell gleichzeitig,
also parallel, berechnet werden können.
4.4 Fehlerberechnung
Man möchte dem Netz nicht beibringen, einen einzigen Eingabevektor
auf einen Ausgabevektor abzubilden. Vielmehr möchte man einen ganzen
Satz von Eingabevektoren auf einen Satz von Ausgabevektoren abbilden.
Zu Anfang muss man sich also Gedanken darüber machen, wieviel und
welche Vektoren assoziiert werden sollen. Bei dem Lernen werden
t Trainingsassoziationen
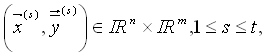
an das Netz angelegt. Die Neuronen des Netzes werden dann im
Feed-Forward durchlaufen. Der dabei entstandene m-dimensionale
Ausgabevektor
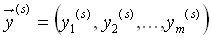 ,
,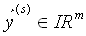
wird von dem aus der Lösungsmenge der zu Verfügung stehenden
Trainingsdaten bekannten Lösungsvektor
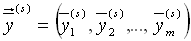 ,
,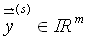
,zunächst subtrahiert, die Fehlerdifferenzen quadriert und dann
summiert (Formel 4.1). Durch die Subtraktion wird die Fehlerdifferenz
bestimmt. Das Quadrieren sorgt dafür, dass die Fehlerdifferenz immer
positiv ist und der Fehler mit einer höheren Gewichtung in
die Berechnung eingeht. Das summieren liefert dann den Gesamtfehler
des Netzes. Das Ziel ist es die Netzparameter so zu wählen das
der Gersamtfehler möglichst klein wird.
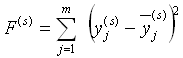 ,
,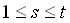 (4.1)
(4.1)
4.5 Fehler-Backpropagation
Nachdem nun der Fehler bekannt ist wird er genutzt, um die
Netzparameter zu optimieren. Das bedeutet, dass ausgehend von
der Ausgabeschicht, die Gewichte und Schwellwerte Schicht für
Schicht verändert werden, bis man zur Eingabeschicht gelangt.
Daher stammt auch der Name Backpropagation. Die eigentlichen
Lernschritte sehen wie folgt aus:
Veränderung der Gewichte der verborgenen Schicht(formal):
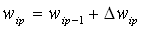 ,
,
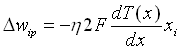 ,
,
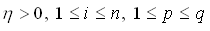 (4.2)
(4.2)
Veränderung der Schwellwerte der verborgenen Schicht(formal):
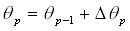 ,
,
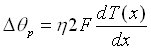 ,
,
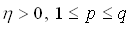 (4.3)
(4.3)
Veränderung der Gewichte der Ausgabe-Schicht(formal):
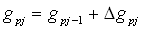 ,
,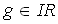
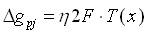 ,
,
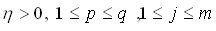 (4.4)
(4.4)
4.6 Allgemeine Berechnung
Allgemein gibt es einen Trainingssatz an Daten.
Dieser Trainingssatz entspricht einer Teilmenge
von dem gesamten Lösungsraum. Die Trainingsdaten
sollten wenn möglich repräsentativ für den gesamten
Lösungsraum sein. Die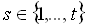 Trainingsassoziationen
Trainingsassoziationen
werden nacheinander an das Netz angelegt. Für jedes
Vektorpaar werden die Gewichte und Schwellwerte
der Rechnung entsprechend optimiert. Die Gewichte
des Ausgangs werden nach der Formel (4.7) optimiert.
Die Gewichte der verborgenen Schicht werden nach
Formel (4.8) verändert und die Schwellwerte der
verborgenen Schicht nach Formel (4.9) geändert.
Bei dem Lernen vergleicht das Netz die Ausgabe,
die es nach Formel (4.6) berechnet und vergleicht
sie mit den Originalwerten. Daraus ergibt sich der
quadratische Fehler. Wenn das letzte Vektorpaar
berechnet wurde, fängt man mit dem ersten Vektorpaar
wieder an. Man verwendet diese Formeln so lange, bis
der quadratische Fehler so klein ist, dass er nicht
mehr relevant ist (Formel 4.5).
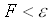 ,
,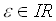 ,
,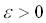 (4.5)
(4.5)
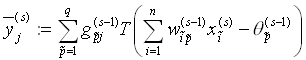 ,
,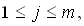 (4.6)
(4.6)
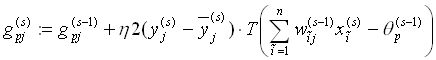 ,
,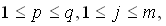 (4.7)
(4.7)
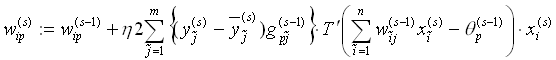 ,
,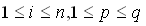 (4.8)
(4.8)
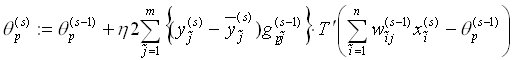 ,
,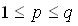 (4.9)
(4.9)
4.7 Bemerkung
Das Feed-Forward-Netz besitzt nur eine verborgene
Schicht. Der Backpropagation-Lernalgorithmus liesse
sich immer noch verwenden, wenn es beliebig viele
verborgene Schichten gäbe. Allerdings sind mehr als
drei Schichten nicht notwendig. Die Verarbeitung zwischen
Schicht eins und zwei entspricht einer Bildung von
Assoziationen, die mehrere Klassen von Vektoren
bilden kann. Vereinfacht gesagt, die Eingabevektoren
werden klassifiziert. Die Verarbeitung zwischen der
zweiten und der dritten Schicht entspricht einer
mehrfachen linearen Regression. Das bedeutet, dass
die bereits in Schicht zwei entstandenen Klassen
durch Kombination beim Lernen den minimalen
quadratischen Fehler finden [1]Rojas|S 194]. In der
Praxis bedeutet dies, dass man zwei Schichten benötigt,
um ein linear separierbares Problem zu lösen. Möchte
man auch nicht linear separierbare Probleme lösen,
benötigt man drei Schichten. Hier stellt sich doch
gleich die Frage, inwieweit man Funktionen nachbilden
kann. Welche Funktionen kann unser Netz überhaupt lösen?
Der russische Mathematiker Kolmogorov hat diese Frage
bereits 1957 beantworten können, denn in diesem Jahr
bewies er mathematisch, dass stetige Funktionen
von n Argumenten immer durch eine endliche Verkettung
von eindimensionalen Funktionen und deren Addition
darstellbar sind. Kolmogorovs Beweis kann man bei
[5]Sprecher(1964) nachlesen. Für ein beliebig komplexes
Netz bedeutet das, dass es nicht auf die Abbildung einiger
Funktionen begrenzt ist, sondern vielmehr kann es jede
stetige Funktion beliebig genau nachbilden.
 Ausgabeneuronen liefern den m-dimensonalen Ausgabevektor
Ausgabeneuronen liefern den m-dimensonalen Ausgabevektor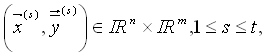
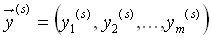 ,
,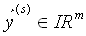
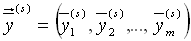 ,
,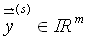
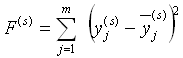 ,
,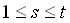 (4.1)
(4.1)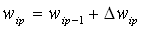 ,
,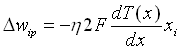 ,
,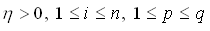 (4.2)
(4.2)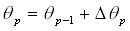 ,
,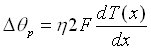 ,
,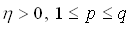 (4.3)
(4.3)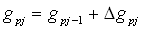 ,
,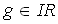
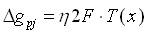 ,
,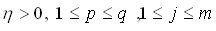 (4.4)
(4.4)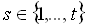 Trainingsassoziationen
Trainingsassoziationen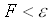 ,
,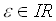 ,
,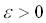 (4.5)
(4.5)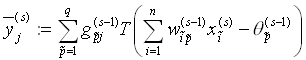 ,
,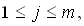 (4.6)
(4.6)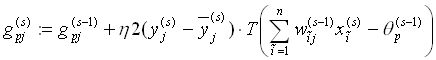 ,
,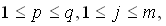 (4.7)
(4.7)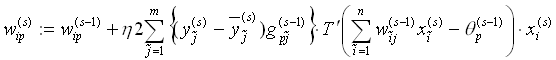 ,
,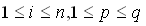 (4.8)
(4.8)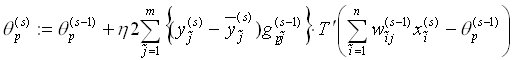 ,
,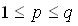 (4.9)
(4.9)