Mathematisches Modell
2.1 Mathematisches Neuron
Definition 2.1 ((formales) Neuron)
Ein (formales) Neuron, im folgenden auch McCulloch-Pitts-Neuron
genannt, ist eine Funktion 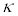 ,
,
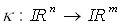 ,
,
gegeben durch:
eine Transferfunktion
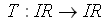 ,
,
einen Gewichtsvektor
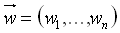
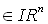
und einen Schwellwert
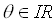 .
.
Konkret wird ein Vektor 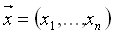
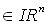 durch das Neuron mittels
durch das Neuron mittels
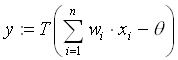
auf den aus m identischen Komponenten bestehenden Vektor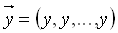
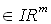
abgebildet, also
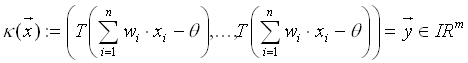 . (vgl.[6], Seite 11)
. (vgl.[6], Seite 11)
2.2 Transferfunktion
Es gibt eine große Menge von Transferfunktionen, von denen
nun einige typische Exemplare betrachtet werden. Die einfachste
Transferfunktion ist die Identität.
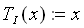 (2.1)
(2.1)
Eine weitere typische Transferfunktion ist die
Heavysidefunktion (Formel 2.2, Abb. 2.2).
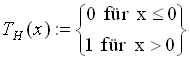 (2.2)
(2.2)
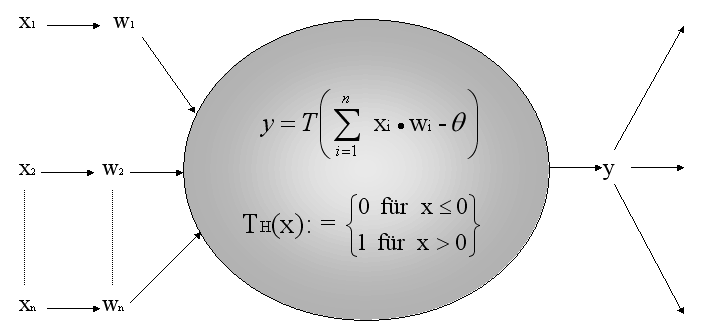
Abb. 2.1 mathematisches Neuron
Die Heavysidefunktion ist nicht differenzierbar und
deshalb für viele mathematische Verfahren ungeeignet.
Die Funktion sollte an jeder Stelle stetig sein.
An der Stelle Null ist die Heavysidefunktion unstetig.
Um mathematische Verfahren, wie z.B. das Gradienten-Verfahren
zu benutzen, verwendet man Funktionen, die der Heavyside-Funktion
ähneln und differenzierbar sind. Um möglichst nahe an der
Heavyside-Funktion zu bleiben,
benutzt man die Fermifunktion (Abb 2.3). Die Fermifunktion zählt
zur Klasse der sigmoiden Funktionen.
Definition 2.2 (Sigmoide Funktion)
Eine Funktion 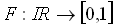 heißt sigmoide oder s-förmige Funktion, wenn sie
heißt sigmoide oder s-förmige Funktion, wenn sie
monoton wachsend und differenzierbar ist und wenn
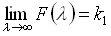 und
und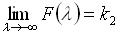 mit
mit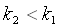 (2.3)
(2.3)
gelten.
Die Fermifunktion lässt sich durch ein beliebig großes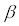 ,
,
beliebig genau an die Heavyside-Funktion anpassen. Das lässt sich
leicht anhand der Formel 2.4 (Fermifunktion) erklären:
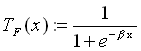
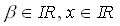
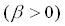 (2.4)
(2.4)
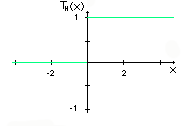
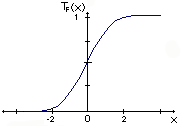
Abb. 2.2 Heavyside-Funktion Abb. 2.3 Fermifunktion mit 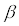 = 2
= 2
Man stellt im Vergleich zur Heavyside-Funktion fest:
Geht x gegen Null, so geht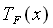 gegen
gegen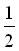 .
.
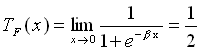 ,
,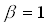 (2.5)
(2.5)
Geht x gegen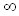 , so geht
, so geht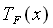 gegen 1. 1 ist die obere Schranke.
gegen 1. 1 ist die obere Schranke.
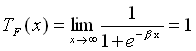 ,
,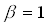 (2.6)
(2.6)
Geht x gegen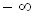 , so geht
, so geht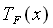 gegen 0. 0 ist die untere Schranke.
gegen 0. 0 ist die untere Schranke.
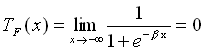 ,
,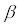 (2.7)
(2.7)
Die Konstante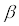 ist die Gewichtung für die Stauchung
ist die Gewichtung für die Stauchung
der Fermifunktion. Je größer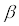 gewählt wird,
gewählt wird,
desto steiler ist die Flanke (Abb. 2.3.x),
und desto näher kommt man an die
Heavyside-Funktion heran.
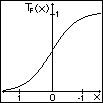
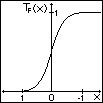
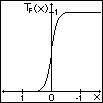
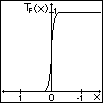
Abb 2.3.x
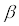 =2,4,8,16
=2,4,8,16
2.3 Erweitertes mathematisches Neuron
Durch die Einführung der sigmoiden Funktionen lässt sich
das mathematische Modell eines Neurons um die Ableitung
der Transferfunktion erweitern (Abb. 2.4).
In unserem Fall betrachten wir die Ableitung der Fermifunktion.
Mit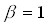 :
:
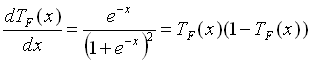 (2.8)
(2.8)
Der Beweis:
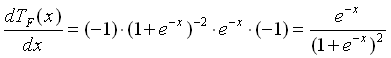
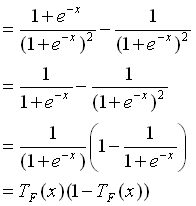
Also gilt
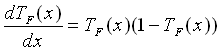 .
.
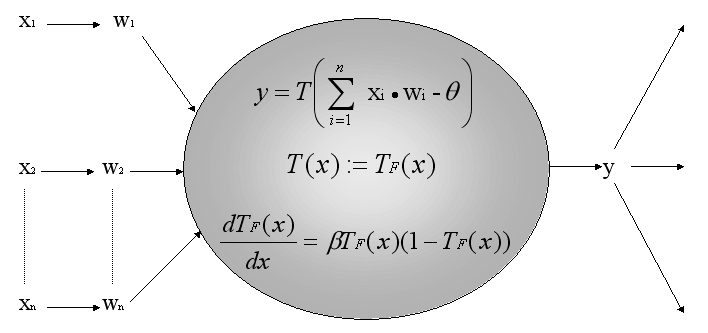
Abb. 2.4: Das erweiterte mathematische Modell eines Neurons
2.4 Dreischichtiges Feed-Forward-Netz
Nachdem die Elemente eines neuronalen Netzes bekannt sind,
wird nun die Netzstruktur an Hand eines dreischichtigen
Feed-Forward Netzes erklärt (Abb. 2.5).
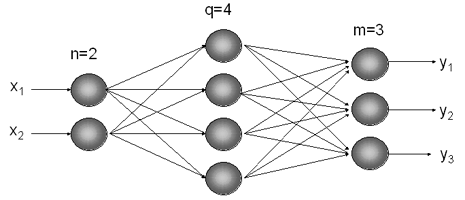
Abb. 2.5: dreischichtige Feed-Forward-Netzstruktur
Das (formale) Feed-Forward-Netz besteht aus Knoten und
Vektoren. Die Knoten entsprechen den (formalen) Neuronen.
Ein Feed-Forward-Netz besitzt eine Eingabeschicht,
die in dem Beispiel aus n=2 Neuronen besteht. Des Weiteren
besteht das Feed-Forward-Netz aus einer verborgenen Schicht,
die hier aus q=4 Neuronen besteht und einer Ausgabeschicht die
hier aus m=3 Neuronen besteht. Bei den Neuronen der ersten und
der letzten Schicht sind die Schwellwerte gleich Null.
Die Neuronen der ersten und der letzten Schicht haben als
Transferfunktion die Identität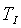 .
.
Definition 2.3 (Dreischichtiges Feed-Forward-Netz)
Das (formale) dreischichtige Feed-Forward-Netz ist ein
neuronales Netz. Das Netz besteht aus Knoten und Vektoren,
die folgende Eigenschaften besitzen:
- Jeder Knoten, der nicht der Netz-Eingabe oder
der Netz-Ausgabe dient, ist ein verborgener Knoten
- Jeder Eingangsknoten hat genau einen Eingangsvektor
- Jeder Ausgangsknoten hat genau einen Ausgangsvektor
- Jeder Eingangsknoten ist mit allen verborgenen Knoten verbunden
- Jeder verborgene Knoten ist mit allen Ausgabeknoten verbunden
- Jeder Knoten entspricht einem (formalen) Neuron
- Die Eingabe- und Ausgabeknoten verwenden die Identität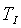 als
als
Transferfunktion
- Die verborgenen Knoten verwenden alle dieselbe Transferfunktion
- Die Gewichte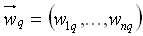 und die Schwellwerte
und die Schwellwerte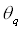 sind die
sind die
Gewichte und Schwellwerte der verborgenen Knoten
- Die Gewichte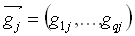 ,
,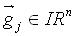 sind die Gewichte der Ausgangsknoten.
sind die Gewichte der Ausgangsknoten.
2.5 Berechnung eines formalen Neurons
Die Aktivierungsfunktion summiert die mit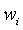 gewichteten Eingänge
gewichteten Eingänge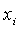
(Formel 2.8).
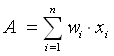 (2.8)
(2.8)
Der nächste Schritt ist, den Schwellwert zu subtrahieren und die
Transferfunktion zu verwenden (Formel 2.9). Man kann den Schwellwert
ersetzen, indem man ein Bias-Neuron benutzt. Das Bias-Neuron ist ein
zusätzliches Neuron. Es besitzt einen festen Eingangswert (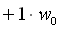 ).
).
Wählt man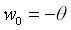 wird der Schwellwert zu einem Gewicht und damit zu
wird der Schwellwert zu einem Gewicht und damit zu
einem Teil der Aktivierungsfunktion (Formel 2.10). Das Ergebnis der
Transferfunktion ist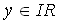 .
.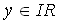 dient als Eingabe für eine nachfolgende
dient als Eingabe für eine nachfolgende
Schicht, daher sind für m-Neuronen, der nachfolgenden Schicht,
ebenfalls m Eingabewerte zu erwarten, d.h.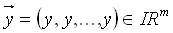 .
.
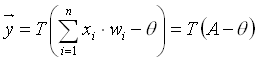 (2.9)
(2.9)
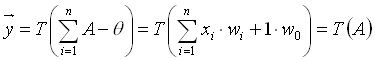 (2.10)
(2.10)
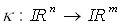 ,
,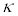 ,
,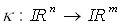 ,
,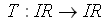 ,
,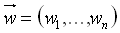
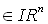
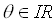 .
.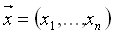
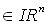 durch das Neuron mittels
durch das Neuron mittels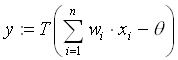
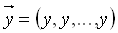
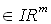
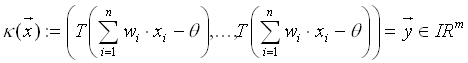 . (vgl.[6], Seite 11)
. (vgl.[6], Seite 11)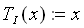 (2.1)
(2.1)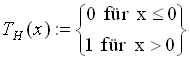 (2.2)
(2.2)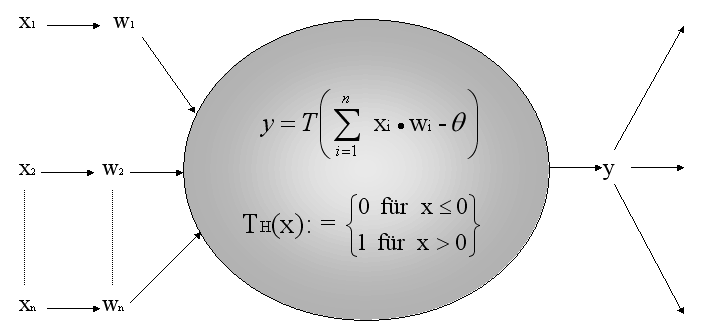
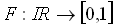 heißt sigmoide oder s-förmige Funktion, wenn sie
heißt sigmoide oder s-förmige Funktion, wenn sie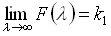 und
und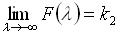 mit
mit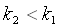 (2.3)
(2.3)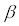 ,
,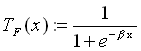
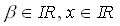
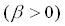 (2.4)
(2.4)

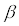 = 2
= 2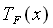 gegen
gegen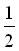 .
.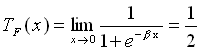 ,
,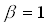 (2.5)
(2.5)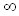 , so geht
, so geht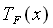 gegen 1. 1 ist die obere Schranke.
gegen 1. 1 ist die obere Schranke.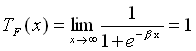 ,
,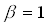 (2.6)
(2.6)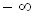 , so geht
, so geht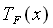 gegen 0. 0 ist die untere Schranke.
gegen 0. 0 ist die untere Schranke.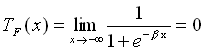 ,
,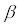 (2.7)
(2.7)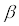 ist die Gewichtung für die Stauchung
ist die Gewichtung für die Stauchung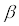 gewählt wird,
gewählt wird,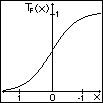



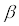 =2,4,8,16
=2,4,8,16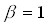 :
: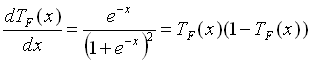 (2.8)
(2.8)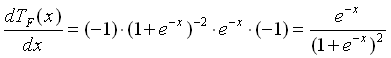
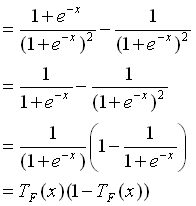
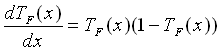 .
.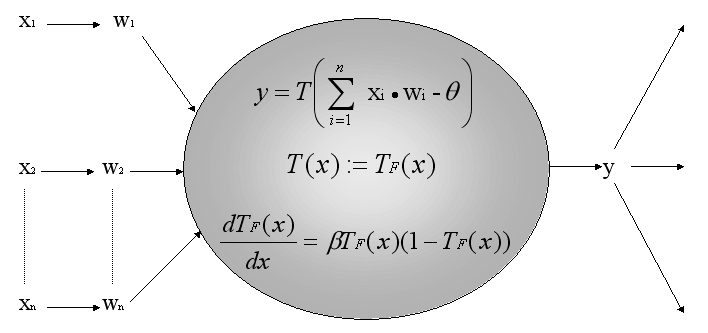

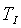 .
.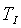 als
als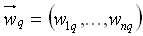 und die Schwellwerte
und die Schwellwerte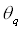 sind die
sind die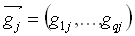 ,
,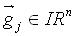 sind die Gewichte der Ausgangsknoten.
sind die Gewichte der Ausgangsknoten.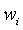 gewichteten Eingänge
gewichteten Eingänge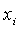
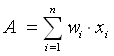 (2.8)
(2.8)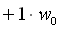 ).
).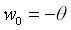 wird der Schwellwert zu einem Gewicht und damit zu
wird der Schwellwert zu einem Gewicht und damit zu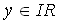 .
.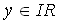 dient als Eingabe für eine nachfolgende
dient als Eingabe für eine nachfolgende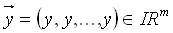 .
.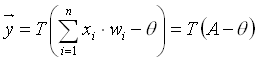 (2.9)
(2.9)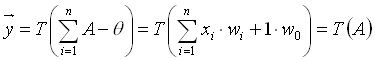 (2.10)
(2.10)